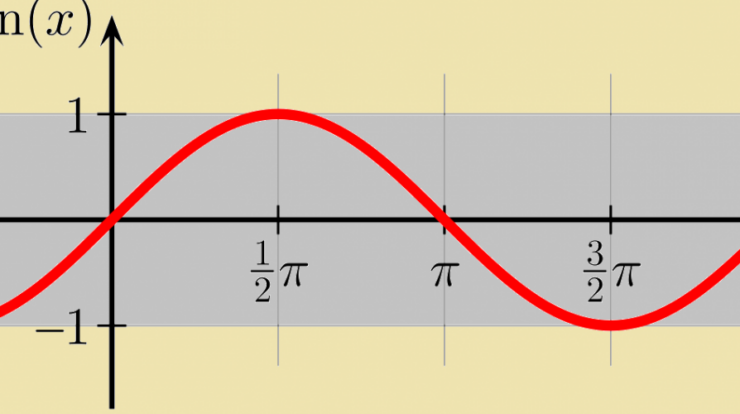
Delving into the realm of trigonometry, we uncover the sine definition, a pivotal concept that unveils the intricate dance of angles and their trigonometric ratios. This mathematical cornerstone finds its applications in a vast array of disciplines, from physics to music, making it an indispensable tool for understanding the world around us.
The sine function, denoted as sin(x), measures the vertical coordinate of a point on the unit circle corresponding to an angle x. It oscillates between -1 and 1, creating a characteristic wave-like pattern that forms the foundation of trigonometry.
Sine Function Definition
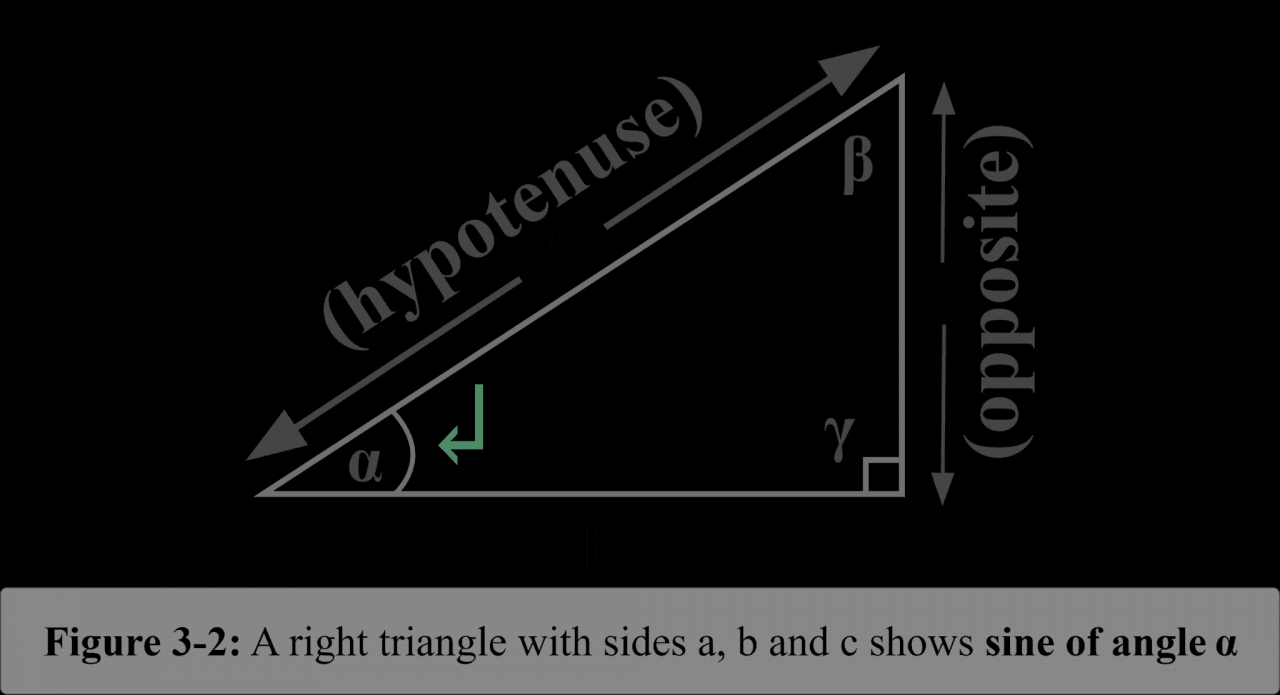
In trigonometry, the sine function is a fundamental trigonometric function that measures the vertical component of a right triangle’s side opposite an angle.
Mathematically, the sine function of an angle θ is defined as the ratio of the length of the side opposite θ to the length of the hypotenuse.
Range and Period
The sine function has a range of [-1, 1]. It is periodic with a period of 2π, meaning it repeats itself every 2π radians.
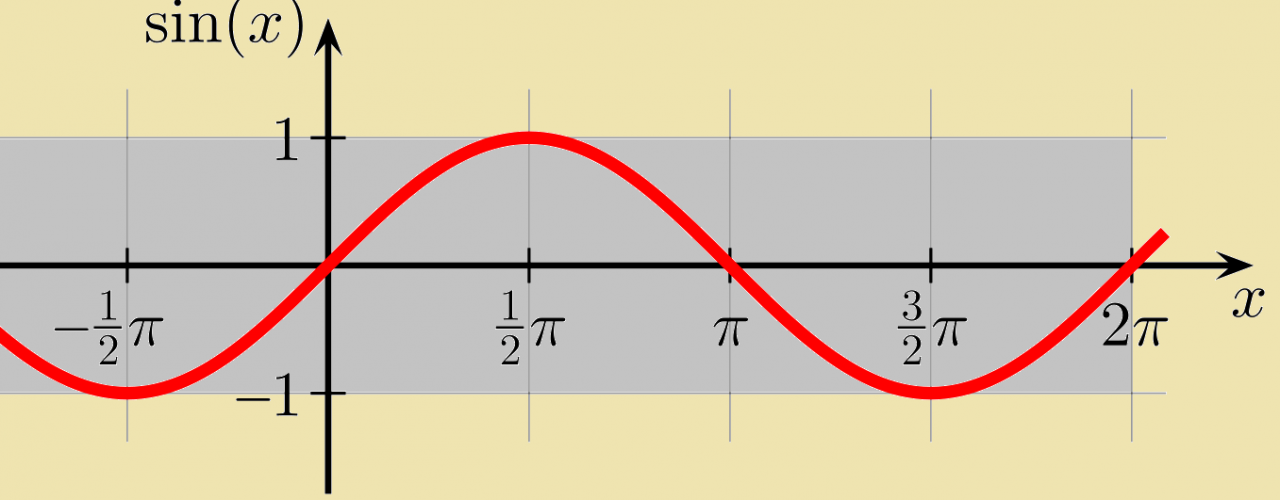
Graph of Sine Function
The graph of the sine function is a smooth, wave-like curve that oscillates between -1 and 1.
The graph is symmetrical about the origin, and its shape is determined by the period and amplitude of the function.
Relationship to Unit Circle
The sine function is closely related to the unit circle. The sine value of an angle θ is equal to the y-coordinate of the point on the unit circle that corresponds to θ.
Example, Sine definition
To graph the sine function, plot the points (0, 0), (π/2, 1), (π, 0), (3π/2, -1), and (2π, 0) on the coordinate plane. Connect these points with a smooth curve to obtain the graph.
Applications of Sine Function
The sine function has numerous practical applications in various fields:
- Physics:Calculating the motion of objects in harmonic motion, such as pendulums and springs.
- Engineering:Analyzing the vibrations of structures, such as bridges and buildings.
- Music:Modeling the sound waves produced by musical instruments.
- Biology:Describing the growth patterns of plants and animals.
Inverse Sine Function: Sine Definition
The inverse sine function, also known as arcsine, is the inverse of the sine function.
It returns the angle whose sine is a given value.
Relationship to Sine Function
The inverse sine function is related to the sine function by the following identity:
“`arcsin(sin(x)) = x“`
Example, Sine definition
To find the angle whose sine is 0.5, use the inverse sine function:
“`arcsin(0.5) = π/6“`
Derivative and Integral of Sine Function
Derivative
The derivative of the sine function is the cosine function:
“`d/dx(sin(x)) = cos(x)“`
Integral
The integral of the sine function is the negative cosine function:
“`∫sin(x) dx =
cos(x) + C
“`
Applications
The derivative and integral of the sine function are used in various applications, such as:
- Calculating the velocity and acceleration of objects in harmonic motion.
- Finding the area under the sine curve.
- Solving differential equations.
Table of Sine Values
A table of sine values for common angles can be used to find sine values quickly.
Here is a table of sine values for angles from 0° to 90°:
| Angle (°) | Sine Value |
|---|---|
| 0 | 0 |
| 15 | 0.2588 |
| 30 | 0.5 |
| 45 | 0.7071 |
| 60 | 0.866 |
| 75 | 0.9659 |
| 90 | 1 |
Last Word
In essence, the sine definition provides a gateway to comprehending the periodic nature of many phenomena in the physical world. From the rhythmic sway of a pendulum to the ebb and flow of tides, the sine function serves as a mathematical lens through which we can decipher the underlying patterns that govern our universe.
FAQ Corner
What is the range of the sine function?
The range of the sine function is [-1, 1].
What is the period of the sine function?
The period of the sine function is 2π.
How is the sine function used in physics?
The sine function is used in physics to model periodic motion, such as the oscillation of a pendulum or the vibration of a spring.